不好意思打扰了大家😭😭。如图🙏🙏我是线段BC，已知线段AB是圆O的直径😭😭，点H在线段AB上，过点H作AB的垂线交圆O于点D😭😭，点E是线段HD的中点🙏🙏，AC与圆O相切，AC=CD，连结CE、BE。求大家帮我知道我和CE和EB的关系🙏🙏是CE+EB>BC还是<还是=并说明理由🙏🙏。求大家帮帮我😭😭感激不尽🙏🙏
151 浏览 · 01-14
0
15
全部评论
只看作者
默认
最新
最早
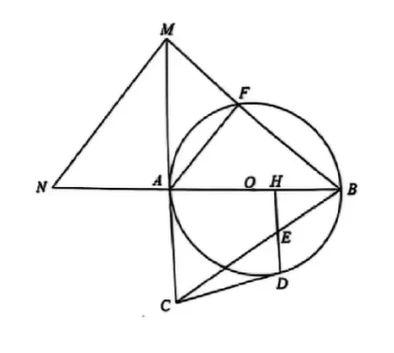
不好意思打扰了大家😭😭。如图🙏🙏我是线段BC，已知线段AB是圆O的直径😭😭，点H在线段AB上，过点H作AB的垂线交圆O于点D😭😭，点E是线段HD的中点🙏🙏，AC与圆O相切，AC=CD，连结CE、BE。求大家帮我知道我和CE和EB的关系🙏🙏是CE+EB>BC还是<还是=并说明理由🙏🙏。求大家帮帮我😭😭感激不尽🙏🙏
151 浏览 · 01-14
0
15
liney
以 A 为原点，AB 为 x 轴正方向，设 AB = 2R，则圆心 O(R,0)，圆方程：
(x-R)^2 + y^2 = R^2
英麒
不语y
蓝云
Ambber
设半径为R，按如下建系：
O(0,0) A(R,0) B(-R,0)
H(x,0) D(x,\sqrt{R^2-x^2}) E(x,\sqrt{R^2-x^2}/2)
设C(R,d)
由AC=CD，得方程：
d^2=(R-x)^2+(d-\sqrt{R^2-x^2})^2
0=R^2-2Rx+x^2+R^2-x^2-2d\sqrt{R^2-x^2}
解得：d=R(R-x)/(\sqrt{R^2-x^2})
)
HE/AC=(\sqrt{R^2-x^2}/2)/d=(R+x)/(2R)=BH/BA
设HD交BC于E'，由相似可得HE'/AC=BH/BA
从而E和E'重合，即HD交BC于E
所以CE+BE=BC
黄金全知者的逆徒
不知道。你问豆包
你也和我一样见过霓虹
，
嘤嘤嘤雪
哼哼哼？哼哼？
欧墨菲斯弟弟欧墨吉利
不知道，总之表达了点某某的思乡之情
全视使
倾颜
眠眠芽
风扶摇
晴天的花海
AC是圆O的切线，故AC 丄 AB；HD ⊥AB，则AC ∥ HD。又AC = CD，E是HD中点，可证C、E、B三点不共线，因此三条线段CE、EB、BC能构成△ CEB。应用三角形三边关系定理，三角形的基本性质为：任意两边之和大于第三边。
在△。 CEB中，CE和EB为两条边，BC为第三条边，因此满足CE + EB > BC。（随便乱说的）